PDEs and Variational Method on 3-D Surfaces and Point Clouds
Introduction
PDEs and variational methods for image processing on Euclidean domains spaces are very well established because they permit to solve a large range of real computer vision problems. With the recent advent of many 3-D sensors, there is a growing interest in transposing and solving PDEs on surfaces and point clouds. We propose a simple method to solve such PDEs using the framework of Partial difference Equations (PdEs) on graphs. This latter approach enables us to transcribe, for surfaces and point clouds, many models and algorithms designed for image processing. [3] [4] [5] [6]
In this approach, 3-D point clouds are represented under the structure of weighted arbitrary graphs. Then we use the framework of Partial difference Equations (PdEs) on weighted graphs to transcribe PDEs and variational methods in the discrete settings of graphs. Conceptually PdEs mimic the PDEs on a general domain by replacing the differential operators by non-local difference operators such as: difference, gradient, divergence, p-laplacian, etc. This graph version of differential operators will enable us to study image processing problems on general graphs representing surfaces and 3-D point clouds.
Regarding the other approaches of the literature, our approach to transpose PDEs on surfaces or point clouds (represented as graphs) has many advantages: no parametrization is needed, no pre-processing is required, no assumption on the surface graph topology is necessary, the use of graph unifies local and non-local processing, and a large range of PDEs can be easily adapted on arbitrary weighted graphs. [1] [2] [3] [4] [5] [6]
Point Cloud Processing
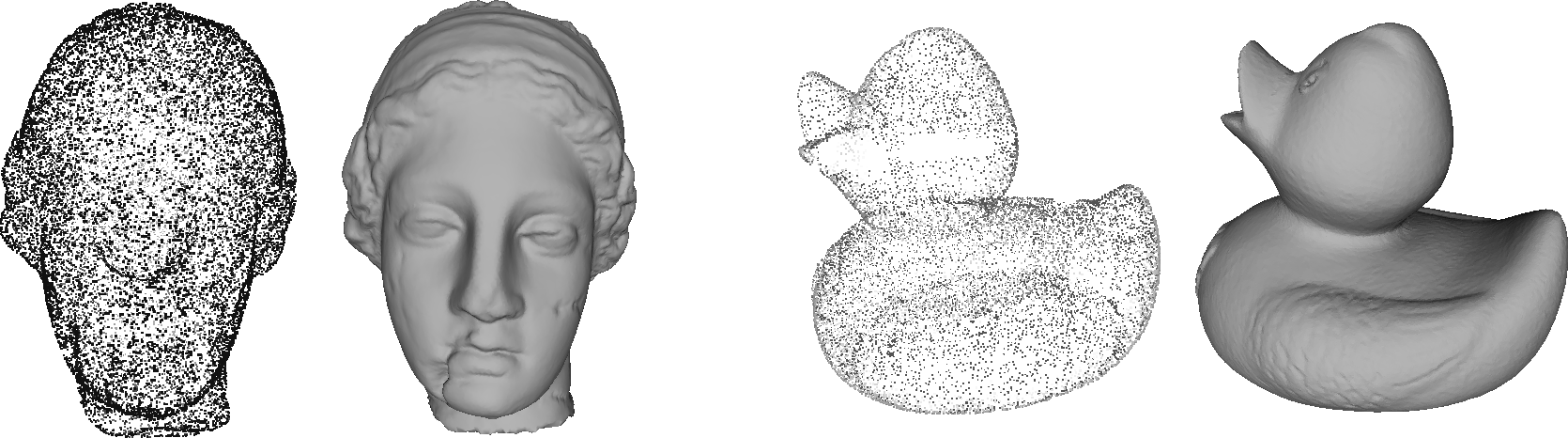
We illustrate our proposal, by considering many problems of image processing on point clouds.Mesh reconstruction from point clouds
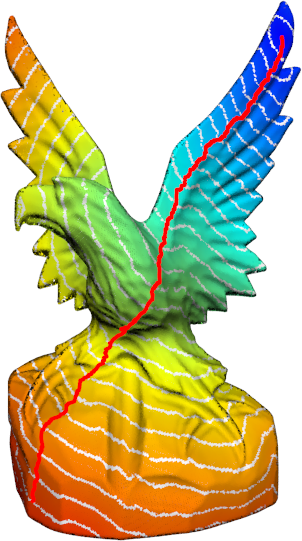
Minimum path / shortest path problem on point clouds
Restoration / Denoising
Inpainting
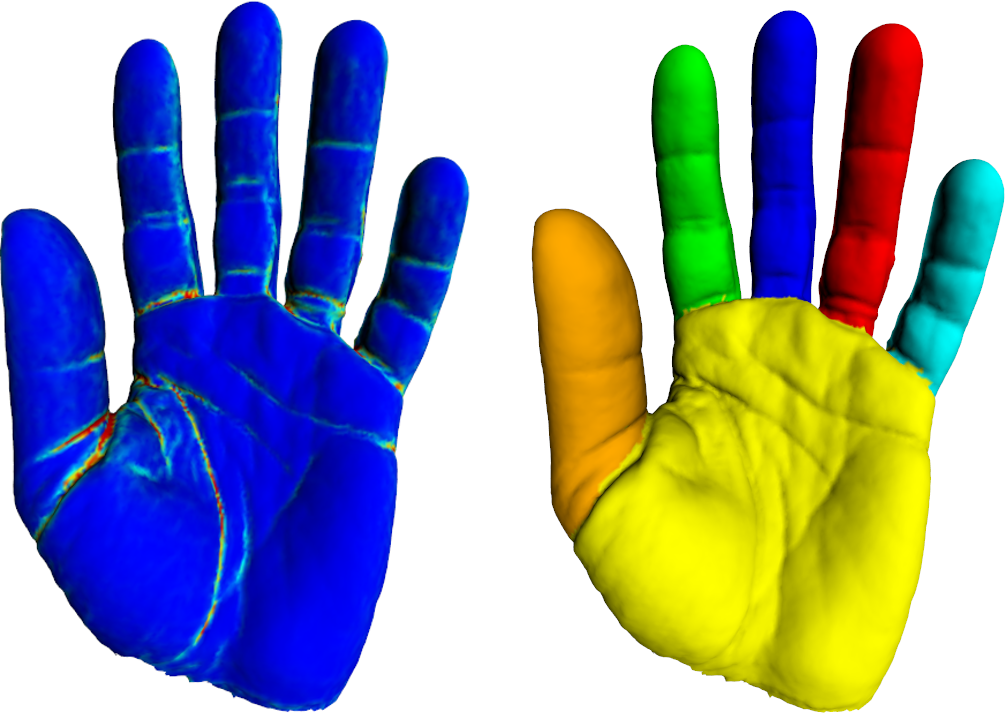
Segmentation
Simplification / Cartoonization
Colorization

Proceduration texture generation
Contributions
A. E. Chakik, A. Elmoataz, X. Desquesnes
 |
In this paper, we propose an adaptation and a transcription of the mean curvature level set equation on the general discrete domain, a weighted graph. For this, we introduce perimeters on graphs using difference operators and define the curvature as the first variation of these perimeters. Then we propose a morphological scheme that unifies both local and nonlocal notions of mean curvature on Euclidean domains. Furthermore, this scheme allows to extend the mean curvature applications to process images, manifolds and data which can be represented by graphs. |
A. E. Chakik, X. Desquesnes, A. Elmoataz
 |
This paper proposes a surface reconstruction approach that is based on fronts propagation over weighted graphs of arbitrary structure. The problem of surface reconstruction from a set of points has been extensively studied in the literature so far. The novelty of this approach resides in the use of the eikonal equation using Partial difference Equation on weighted graph. It produces a fast algorithm, which is the main contribution of this study. It also presents several examples that illustrate this approach. |
M. Toutain, A. Elmoataz, F. Lozes, A. Mansouri
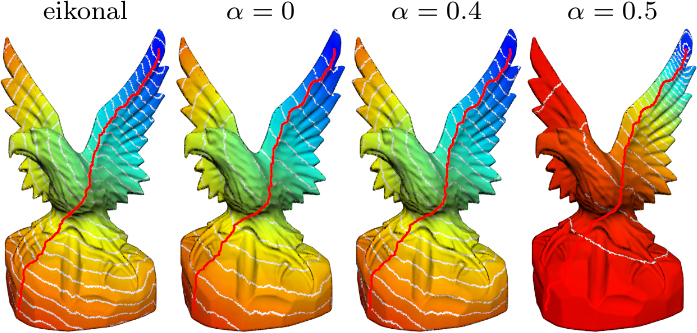 |
In this paper we propose an adaptation of the ∞-Poisson equation on weighted graphs, and propose a finer expression of the ∞-Laplace operator with gradient terms on weighted graphs, by making the link with the biased version of the tug-of-war game. By using this formulation, we propose a hybrid ∞-Poisson Hamilton-Jacobi equation, and we show the link between this version of the ∞-Poisson equation and theadaptation of the eikonal equation on weighted graphs. Our motivation is to use this extension to compute distances on any discrete data that can be represented as a weighted graph. Through experiments and illustrations, we show that this formulation can be used in the resolution of many applications in image, 3D point clouds, and high dimensional data processing using a single framework. |
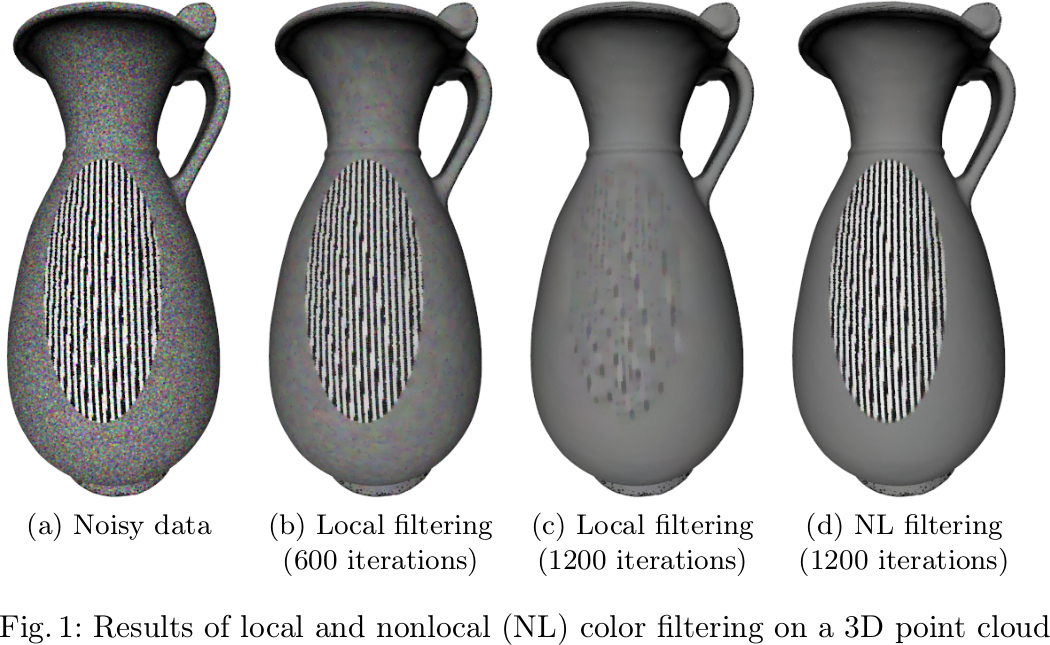 |
Minimal surface problems play not only an important role in physics or biology but also in mathematical signal and image processing. Although the computation of respective solutions is well-investigated in the setting of discrete images, only little attention has been payed to data of more complicated topology, e.g., surfaces represented as meshes or point clouds. In this work we introduce a novel family of discrete total variation seminorms for weighted graphs based on the upwind gradient and give an efficient minimization algorithm to perform total variation denoising. Furthermore, we demonstrate how to utilize the latter algorithm to uniquely solve minimal surface problems on graphs in a unified framework. To show the universal applicability of this approach, we illustrate results from filtering and segmentation of point cloud data. |
F. Lozes, A. Elmoataz, O. Lézoray
 |
With the advance of three-dimensional (3-D) scanning technology, the cultural heritage community is increasingly interested in 3-D scans of cultural objects such as antiques, artifacts, and heritage sites. Digitization of these objects is commonly aimed at heritage preservation. Since 3-D color scanning has the potential to tackle a variety of traditional documentation challenges, the use of signal processing techniques on such data can be expected to yield new applications that are feasible for the first time with the aid of captured 3-D color point clouds. Our contributions are twofold. First, we propose a simple method to solve partial differential equations (PDEs) on point clouds using the framework of partial difference equations (PdEs) on graphs. Second, we survey several applications of 3-D color point cloud processing on real examples for which signalprocessing researchers can develop tools that can be valuable for museum specialists. The results of these methods have been reviewed by experts in the arts and found promising. |
F. Lozes, A. Elmoataz, O. Lézoray
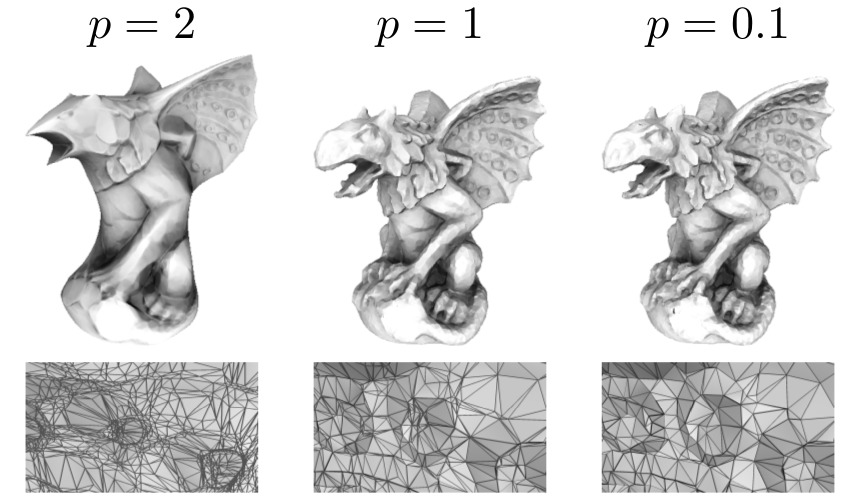 |
PDEs and variational methods for image processing on Euclidean domains spaces are very well established because they permit to solve a large range of real computer vision problems. With the recent advent of many 3D sensors, there is a growing interest in transposing and solving PDEs on surfaces and point clouds. In this paper, we propose a simple method to solve such PDEs using the framework of Partial difference Equations (PdEs) on graphs. This latter approach enables us to transcribe, for surfaces and point clouds, many models and algorithms designed for image processing. To illustrate our proposal, three problems are considered: p-Laplacian restoration and inpainting, PDEs Mathematical Morphology, and active contours segmentation. This work was funded under a Ph.D. grant of the regional council of Lower-Normandy. |
A. Elmoataz, M. Toutain, D. Tenbrinck
 |
In this paper we introduce a new family of partial difference operators on graphs and study equations involving these operators. This family covers local variational p-Laplacian, ∞-Laplacian, nonlocal p-Laplacian and ∞-Laplacian, p-Laplacian with gradient terms, and gradient operators used in morphology based on the partial differential equation. We analyze a corresponding parabolic equation involving these operators which enables us to interpolate adaptively between p-Laplacian diffusion-based filtering and morphological filtering, i.e., erosion and dilation. Then, we consider the elliptic partial difference equation with its corresponding Dirichlet problem and we prove the existence and uniqueness of respective solutions. For p = ∞, we investigate the connection with Tug-of-War games. Finally, we demonstrate the adaptability of this new formulation for different tasks in image and point cloud processing, such as filtering, segmentation, clustering, and inpainting. |